以下文章來源於林驥 ,作者林驥
1. 為什麼學習方差分析?
學習方差分析的原因主要有以下幾點:
① 發現資料規律
透過方差分析,可以探索資料之間的關係,確定不同因素對變數的影響是否顯著,從而幫助我們發現資料背後的規律。
② 解讀統計結果
方差分析提供了一種解讀資料統計結果的方法,進而有助於更深入地理解和洞察事業的實際情況。
③ 提升決策品質
方差分析可以幫助我們更加科學地處理資料,確定哪些因素對事業有重要影響,提高決策的科學性和準確性。
2. 什麼是方差分析?
方差分析(Analysis of Variance,簡稱 ANOVA)是一種統計方法,用於檢驗不同因素對資料變異的影響是否顯著,所以也被稱為「變異數分析」。
假設有 2 種提升銷售收入的策略,如何判斷它們是否存在顯著的差異?
按照傳統的分析方法,就是把 2 種策略都嘗試一遍,然後對比二者的銷售收入,看哪個銷售收入高,就說哪種策略更有效。
然而,這種傳統的分析方法並不嚴謹。為了讓分析的過程更加科學,我們可以運用假設檢驗的方法,先提出假設,再統計檢驗,最後做出判斷。
方差分析的核心思想是把總體差異分解為組間差異和組內差異,然後比較不同成分對總體的影響是否顯著。
方差分析有 3 種不同的類別:
① 單因素方差分析
單因素方差分析用於研究 1 個因素對變數的影響。
例如,分析學歷對工資收入的影響。
② 雙因素方差分析
雙因素方差分析用於研究 2 個因素對變數的影響。
例如,分析學歷和年齡對工資收入的影響。
③ 多因素方差分析
多因素方差分析用於研究 3 個或 3 個以上因素對變數的影響。
例如,分析學歷、年齡、性別對工資收入的影響。
3. 怎麼運用方差分析?
下面舉一個簡單的例子,用來演示方差分析的基本步驟。
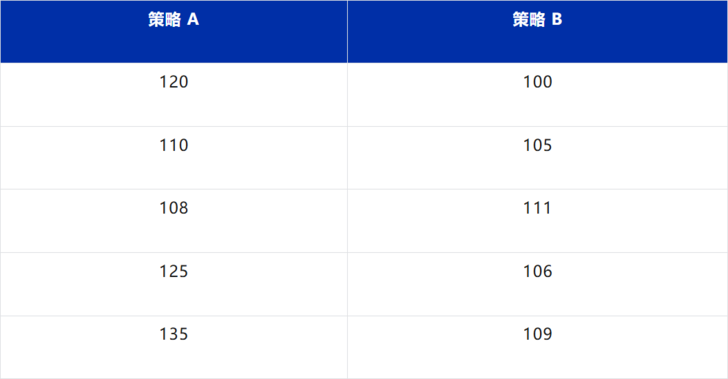
假設有 2 種促銷策略,對應每天的銷售額資料如下:
問:這 2 種促銷策略的效果差異是否顯著?
首先,我們明確資料分析的目標,是要判斷 2 種促銷策略是否存在統計學意義上的顯著差異,而不是某個人的主觀感受。
其次,我們把總體差異分解為組間差異和組內差異,其中組間差異是指不同促銷策略之間的差異,組內差異是同一種促銷策略內部的差異。
比如,策略 A 下面不同日期的銷售額資料,就屬於組內差異,這種差異不是由促銷策略引起的,而是由其他因素引起的。
如果組內差異很大,而組間差異卻很小,那麼就說明促銷策略對銷售的影響很小。
反之,如果想要說明銷售額與促銷策略有關,那麼就需要組間差異足夠大,且組內差異足夠小。
我們不必記住方差分析的計算公式,只需要利用 Excel 的資料分析功能,就能快速完成方差分析,具體操作步驟如下:
① 準備資料
開啟 Excel 軟體,把上面的資料輸入進去,假設放在 A1:B6 單元格區域。
② 分析工具
在 Excel 選單欄中,選擇【資料】→【資料分析】。
如果看不到【資料分析】選項,則需要先載入分析工具庫。在Excel 中以此點選:【檔案】→【選項】→【載入項】,轉到 Excel 載入項頁面,勾選其中的【分析工具庫】。
③ 方差分析
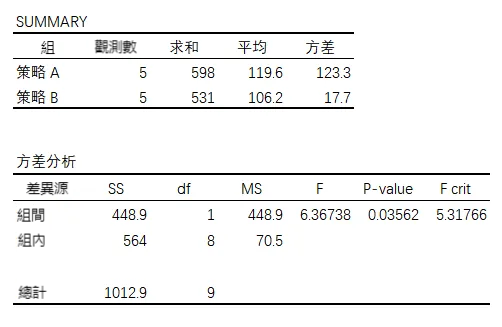
在【資料分析】對話方塊中,選擇【方差分析:單因素方差分析】,點選確定之後,選擇輸入區域為 $A$1:$B$6,勾選【標誌位於第一行】,再點選確定,Excel 將自動生成方差分析的結果如下:
其中 SS 代表平方和,df 代表自由度,MS 代表均方和,F 值是組間差異與組內差異的比值,P-value 用於確定顯著性的機率,F crit 是指 F 臨界值。
這些統計學概念看起來比較複雜,但我們其實不必深究其中的含義,只要知道如何解讀分析的結果:當 P-value < 0.05 或 F > F crit 時,代表有顯著差異。
所以,從上面的結果可以看出,兩種促銷策略存在顯著差異。