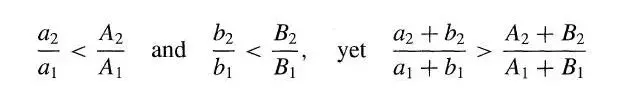以下文章來源於首席數據科學家 ,作者NK冬至
資料會說謊?資料同行們應該對這個話題都有較多的感觸。今天咱們一起聊聊一個比較有意思、但經常忽略的數學現象:辛普森悖論,看一看這回資料到底是怎麼說謊的。
01 到底哪個結論是對的
我們來看一個案例。
我們想判斷醫院A和醫院B哪家醫院的死亡率更低,希望透過死亡率判斷醫院的診治水平。
統計A和B的總體死亡率,我們發現A的死亡率是36%(假設總病人100,死亡36人),B的死亡率是40%(假設總病人100,死亡40人)。
假設我們上述的資料統計口徑都是完全一致的,沒有口徑上的差異,那是不是可以得出結論:B醫院的診治死亡率更高?再延伸一下,那是不是代表B醫院的治療水平差,畢竟死亡率高嘛!
如果是這樣的推理邏輯,其實存在了巨大的漏洞。我們將A和B醫院的病人按照危重程度進行二分類,分為危重病人和輕症病人,再來看一看資料情況,如下圖:
透過上圖我們發現,A醫院的危重病人比重較低,100個人中只有20個,剩下的80個病人都是輕症病人;而B醫院的情況恰恰相反,80個危重病人,20個輕症病人。無論是A醫院還是B醫院,重症病人的死亡率都很高,A醫院甚至達到了100%;而輕症病人的死亡率相對較低,B醫院0死亡。
縱向對比發現,無論是重症病人、還是輕症病人,B醫院的死亡率都是要低於A醫院的。但是由於B醫院的重症病人比重遠大於A醫院,導致了總體的死亡率高。
因此,我們到底要說B醫院的診治死亡率是高呢,還是低呢?
如果單純從總體資料上得出結論:B醫院的總體死亡率更高,這個從統計上沒問題,但是並不代表B醫院的治療水平差,因為從細分結構上看,B醫院的水平都更高。
這就是典型的辛普森悖論:即總體得出的結論和拆分後分項得出的結論,完全相反。
02 為啥會出現這種現象
有沒有覺得很神奇。那為啥會出現這種現象呢?我們從數學和通俗兩個角度分別看一下。
(1)資料角度
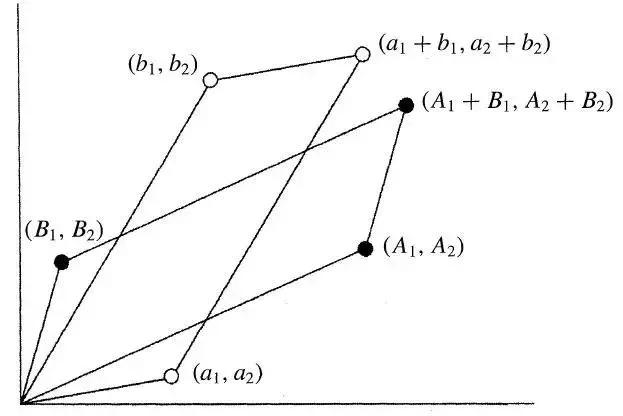
我們先從數學的角度來看一看。其實可以用下面的圖形化來表示:
上圖中的3個黑點代表了A醫院,3個白點代表了B醫院。右上側的黑點和白點代表了A醫院和B醫院的總體,適應於向量的加法,是由兩個子向量(即重症和輕症)相加得到。x軸是患病人數,y軸是死亡人數。因此,每個向量的斜率代表了死亡比率。
透過上圖,我們可以發現:
子部分的比例大小,彙總後的整體大小關係並無絕對性。
再看一個散點圖,也是很直觀地說明了這一點:
上面的散點圖,如果不拆分到子部分,單純看x和y,明顯是負相關。但如果透過顏色第三個維度進行區分,明顯發現x和y是正相關的。
(2)通俗實踐角度
我們從通俗實踐的角度,看看為啥會出現辛普森悖論。
簡而言之:當我們對總體進行了第三個維度的拆分後(也就是我們常說的下鑽),由於不同分析物件在第三維度的比例結構有差別,最終導致了悖論現象的發生。
換句話說,如果兩個分析物件,在所有的維度拆分上的比例結構都一致,那麼也就不會出現辛普森悖論。
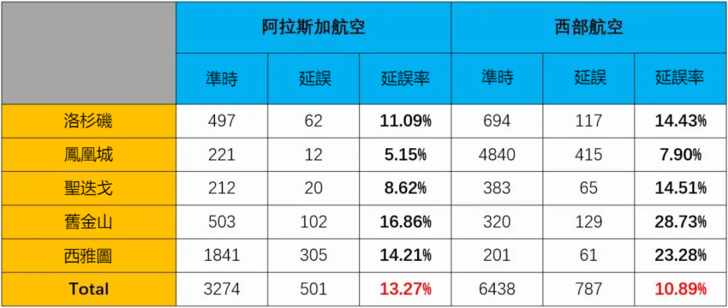
但通常來講,實踐中總會有差別的結構維度,因此出現該悖論也是機率不低的。往往沒發現結構性差異,是因為關鍵的拆解維度沒有被找到,而不是不存在。比如下面這個航空公司準點率的例子:
總體延誤率明顯是西部航空更低,但是拆分到起飛機場維度,發現每個機場的阿拉斯加航空的延誤率都低於西部航空。主要的干擾資料就是鳳凰城機場,西部航空的航班異常多,拉低了整體的延誤率。
但是拆分機場這種關鍵維度,有時候是不是也不太能想到。只有對事業充分了解、對資料足夠敏感,才能發現這其中的問題吧~
03 一些啟示
透過上面的案例及分享,不知道各位朋友是不是有了一些自己的想法。
其實多年前我搞資料分析的時候,確實遇到過這個問題。當初自己不知道辛普森悖論,一直覺得是自己資料算錯了。結果核查了好幾遍發現資料沒問題,但就是結論和直觀的感覺相悖。然後我就簡單證明了一下,確實會出現這個現象。後來才知道這個是辛普森悖論。
一方面,希望各位朋友以後再碰到這種彙總統計資料的時候,保留一顆質疑的心,極有可能是隱瞞了關鍵維度而得出了誤導性的結論。另一方面,各位朋友自己在做資料分析的時候,切記多多做下鑽、多多嘗試不同的維度進行分析。單單透過彙總資料得出的結論很有可能是和真相背道而馳的。
當然,這也給有些喜歡透過資料“說謊”的人,留下了後門。但這不應該是我們資料人所追求的。